纯电容复阻抗公式推导

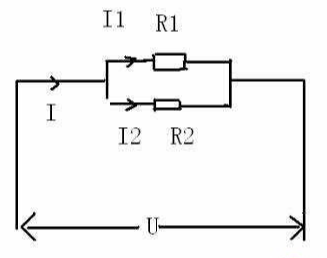
复阻抗的定义

　　在关联参考方向下，正弦交流电路中任一线性无源单口的端口电压相量与电流相量的比称为该单口的复阻抗，用Z表示，即：Z==|Z|《Ψz。显然复阻抗也是一个复数，但它不在是表示正弦量的复数，因而不是相量。在电路图中有时用电阻的图形符号表示复阻抗。

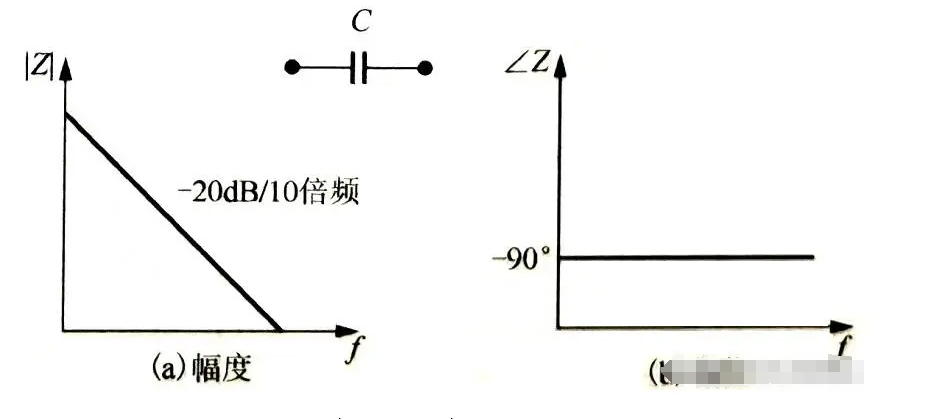
　　复阻抗是反映一段无源电路或无源二端网络电性质的物理量。在交流电路的复数解法中，把电压电流等简谐量都用其对应复数表示，分别称为复电压、复电流。一段无源电路上复电压、复电流的比称为复阻抗。复阻抗的辐角等于电压电流的位相差，称为阻抗角。复阻抗的代数式表为Z=r+jX。式中复阻抗的实部r称为有功电阻，复阻抗的虚部X称为电抗。纯电阻的复阻抗Z=R，纯电感元件的复阻抗Z=jωL，其量值XL=ωL，称为感抗。纯电容元件的复阻抗Z=1/jωC=-j1/ωC，其量值Xc=1/ωC称为容抗。

　　复阻抗的概念可以推广到任一无源二端网络，无源二端网络上复电压与复电流的比称为无源二端网络的复阻抗，表为Z=U/I。式中U为无源二端网络两个引出线端之间的电压复有效值；I是通过二端网络的电流复有效值。复阻抗既反映了这段电路阻抗的大小（用复阻抗的模表示），又反映在这段电路上电压与电流间的位相差（用复阻抗的辐角表示）。所以复阻抗比阻抗有更丰富的内容。

　　由复阻抗的定义式Um=ImZ或U=IZ，它与直流欧姆定律有相同的形式，称为复数形式的欧姆定律。引入复电压、复电流、复阻抗后使得交流电路规律的表达式变得非常简洁。

　　RLC串联电路的复阻抗

　　RLC串联电路

　　电阻R、电感L、电容C的串联电路如右图所示，设各元件电压uR、uL、uC的参考方向均与电流的参考方向关联，由KVL得：u=uR+uL+uC。由于都是线性元件，所以各电压以及电路端电压端电流都是同频率的正弦量，故各电流和电压都可以用相量表示为：

　　上式表明，电阻上电压与电流相同，电感电压超前于电流90度，电容电压滞后于电流90度。以电流相量为参考相量，即I=I《0，绘出电压、电流的相量图。

　　图中U与UR、UX（=UL+UC）组成一个直角三角形，称为电压三角形，其中ΨZ=Ψu-Ψi为电压超前于电流的相位差。通过电压三角形得到：

　　根据UL和UC之间的关系，可以分为三种情况讨论：

　　当UL–UC》0，即UL》UC时，Ψz》0，电压超前于电流，电路呈电感性；

　　当UL–UC《0，即UL《UC时，Ψz《0，电压滞后于电流，电路呈电容性；

　　若UL–UC=0，即UL=UC时，Ψz=0，电压与电流相同，电路呈电阻性；

　　RLC串联电路VCR的相量形式

　　将各元件VCR的相量形式代入式U=UR+UL+UC得：

　　UR=RI+jXLI-jXCI=［R+j（XL-XC）］I=（R+jX）I

　　其中，X=XL-XC称为电路的电抗。这就是RLC串联电路VCR的相量形式。

　　RLC串联电路的复阻抗

　　由RLC串联电路VCR的相量形式和复阻抗的定义可得RLC串联电路的复阻抗与电源频率及元件参数的关系为：

　　复阻抗是复数，因而可以用复平面上的有向线段来表示，如图所示：

　　图中复阻抗Z与R、jX组成一个直角三角形，称为阻抗三角形，显然，阻抗三角形与电压三角形是相似的。由阻抗三角形可以得到下面关系：

　　及R=|Z|cosΨzX=XL-XC=|Z|sinΨz有式可以得出：

　　当X》0即XL》XC时，Ψz》0，电压超前于电流，电路呈现感性；当X《0即XL《XC时，Ψz《0，电压滞后于电流，电路呈容性；若X=0即XL=XC时，Ψz=0，电压与电流同相，电路呈电阻性

　　复阻抗的计算公式

　　复阻抗等于关联参考方向下，端口电压相量和端口电流相量的比值，用符号Z表示，即

　　1、呈感性

　　2、呈容性

　　3、呈阻性

　　例题：